Exercice d’entraînement – Théorème de Pythagore
Un véliplanchiste très expérimenté fait une sortie en mer en jour de tempète où le vent atteint la vitesse de 100 km/h. À cette vitesse, la pression p du vent est estimée à 500 Pa.
Le but de l’exercice est de calculer la valeur exacte de la force exercée par le vent sur la toile dont le shéma est donné ci-dessous.
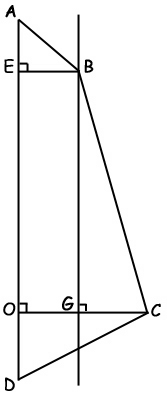
Partie 1 : Calcul de l’aire réelle de la voile
On donne AB=99 cm, DC = 200 cm, AE=70 cm, EO = 240 cm et OD = 120 cm.
1. Donner la nature des triangles ABE, CDO et BGC. Justifier les réponses.
ABE est un triangle rectangle en E car Ê est un angle droit.
CDO est un triangle rectangle en O car Ô est un angle droit.
(BG) est perpendiculaire à (GC) donc G est un angle droit et BGC est un triangle rectangle en G.
2. a) Calculer en cm les longueurs de EB, OC. Arrondir le résultat à l’unité.
Dans le triangle CDO rectangle en O.
D’après le théorème de Pythagore :
CD2 = OD2 + OC2
OC2 = CD2 – OD2
OC2 = 2002 – 1202
OC2 = 40000 – 14400 = 25600
donc OC = 160 cm
De même, EB = √4901
EB ≈ 70 cm
b) Calculer en cm la longeur de GC. Arrondir le résultat à l’unité.
O, G et C sont alignés dans cet ordre donc : GC = OC – OG
Or OEGB est un quadrilatère qui possède 3 angles droits, donc c’est un rectangle.
donc EB = OG ≈ 70 cm et OE = BG = 240 cm d’où GC ≈ 160 – 70
GC ≈ 90 cm
3. Calculer en cm2 l’aire des trois triangles ABE, CDO et BCG.
Calcul de l’aire ABE
A (ABE) = (AE x EB ) : 2
…………… ≈ (70 x 70 ) : 2
…………… ≈ 2450 cm2
Calcul de l’aire CDO
A (CDO) = (OD x OC) : 2
…………… = (120 x 160 ) : 2
…………… ≈ 9600 cm2
Calcul de l’aire BCG
A (BCG) = (GB x GC ) : 2
…………… ≈ (90 x 240 ) : 2
…………… ≈ 10 800 cm2
Les aires de ABE, CDO et BCG sont respectivement 2450 cm2, 9600 cm2, 10 800 cm2.
4. Calculer en cm2 l’aire du rectangle EBGO.
A (EBGO) = EB x OE
……………… ≈ 70 240
……………… ≈ 16 800 cm2
L’aire de EBGO est 16800 cm2.
5. Calculer en cm2 l’aire de la voile.
Avoile = A (ABE) + A (CDO) + A (BCG) + A (EBGO)
………. ≈ 2450 + 9600 + 10800 + 16800
………. ≈ 39650 cm2
6. Exprimer l’aire de la voile en m2
Avoile = 3,965 m2
Partie 2 : Calcul de la force exercée par le vent
La force exercée par le vent est donnée par la relation : F = p x S où F est la valeur de la force en newton (N), S est la surface de la voile en mètre carré (m2) et p la pression en pascal (Pa).
Calculer la valeur de la force F, agissant sur la voile lorsque le vent atteint la vitesse de 100 km/h, c’est-à-dire que p = 500 Pa. Arrondir le résultat à l’unité.
F = p x S
…≈ 500 x 3,965
…≈ 1983 N
La valeur de la force exercée sur la voile est de 1983 N.


